■趣味の数学問題集・Ａ問題の答

  1. 仮定より
    ∠ABC＝∠ACB･･･①
    ∠FDM＝∠EDM･･･②
    である。
    四角形GHIJにおいて，
    ∠GHI＝∠BHD
    ＝∠ABC－∠HDB
    ＝∠ACB－∠JDC（①，②より）
    ＝∠DJC
    1つの内角が対角の外角に等しいので
    四角形GHIJは円に内接する。
    よって，4点G，H，I，Jは同一円周上にある。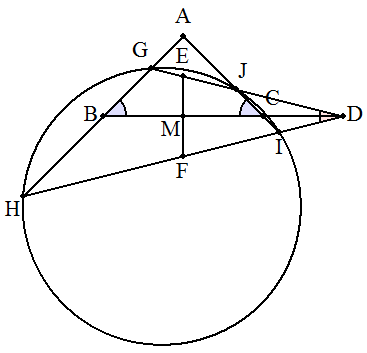

  2. (1)　10√10/9
    (2)　50√39/27
    ※参照→こだわり数学　72.円に内接する四角形に内接するひし形について

  3. FA＝10
    （解答）
    △PAB∽△PEDより　AB/ED＝PA/PE･･･①
    △PCD∽△PAFより　CD/AF＝PC/PA･･･②
    △PEF∽△PCBより　EF/CB＝PE/PC･･･③
    ①，②，③を辺々掛け合わせると
    AB・CD・EF/(BC・DE・FA)＝1
    ∴AB・CD・EF＝BC・DE・FA
    この式に与えられた条件を代入すると
    14・20・12＝16・21・FA
    よって　FA＝10･･･（答）
    （参考）六角形の外接円の半径の近似値：15.67613299

  4. （解答例）
    1. 2015＝(1×2＋3)×(456－7×8＋√9)
    2. 2015＝(1×2＋3－4＋5×6)(－7＋8×9)
    3. 2015＝(12－3＋4)×5×(6×7－8－√9)
    4. 2015＝1234＋(5!－6)×7－8－9
    5. 2015＝12×34×5＋6－7－8×√9
    6. 2015＝(1×2＋34)×56＋(7－8)9
    7. 2015＝－1＋(2－3＋4－5＋6)×7×8×9
    8. 2015＝1＋2×(3＋√4×5＋6)×(7×8－√9)
    9. 2015＝1＋(23＋4＋5＋6)×(7×8－√9)
    ※他を見つけた方，ご連絡をお願いします。

  5. (1)　S＝(1/4)√{3(b2c2＋c2a2＋a2b2)－2abc(a＋b＋c)}
    (2)　V＝(√2/12)abc
    (例)　a＝2，b＝3，c＝4のとき，S＝5√3/2，V＝2√2
    解答→こちら

  6. (1)　0
    (2)　1

  7. 最小値　1/7100（a＝22，b＝31のとき）

  8. a＝74，b＝61

  9. x＝19，y＝16
    解答→こちら

  10. (1)　8/3
    (2)　(n－1)(30n－47)/6n

  11. (m，n)＝(6，8)，(35，49)，(204，288)
    他に，(1189，1681)，(6930，9800)，(40391，57121)，(235416，332928)
    (1372105，1940449)，(7997214，11309768)など
    一般に，k>1として，
    m＝{(1＋√2)2k－(1－√2)2k}/(4√2)
    n＝{(1＋√2)2k＋(1－√2)2k－2}/4
    で与えられる。

  12. 158　余り128
    79　余り49

  13. (-a2+b2+c2)(a2-b2+c2)(a2+b2-c2)√{(a+b+c)(-a+b+c)(a-b+c)(a+b-c)}/(8a2b2c2)
    （補）△ABC＝Sとおくと，六角形の面積は，4ScosAcosBcosCとなる。
    解答→こちら

  14. S=(a1b2c3+a2b3c1+a3b1c2-a1b3c2-a2b1c3-a3b2c1)2/2|(a1b2-a2b1)(a2b3-a3b2)(a3b1-a1b3)|
    行列式を用いて表すと，


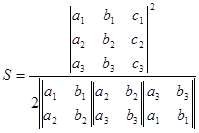
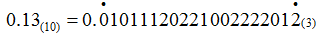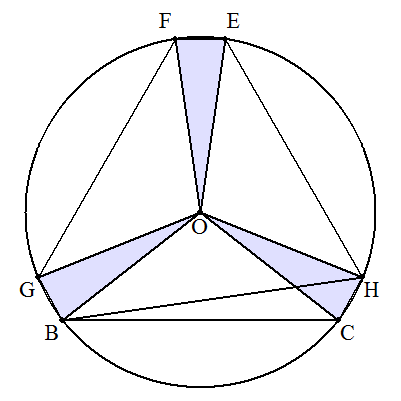
  15. (1)　
    (2)　こちら

  16. 円の中心をOとし，半径をrとする。
    3個の底辺2の二等辺三角形と3個の底辺11の二等辺三角形に分ける。
    次に，6個の二等辺三角形を右の図のように交互に並べ替える。
    ∠BOH＝120°，∠BCH＝120°である。
    △OBHと△CHBについて，BHは共通であるから，余弦定理より
    BH2=2r2-2r2cos120°=112+22-2・11・2cos120°
    r2=49
    r>0より　r=7･･･（答）
    （補足）
    一般に，AB=BC=CD=a，DE=EF=FA=bのとき，r=√{(a2+ab+b2)/3}である。
    整数になる例　(a，b，r)＝(1，22，13)，(11，26，19)

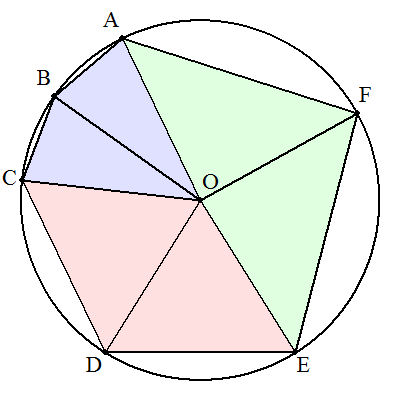
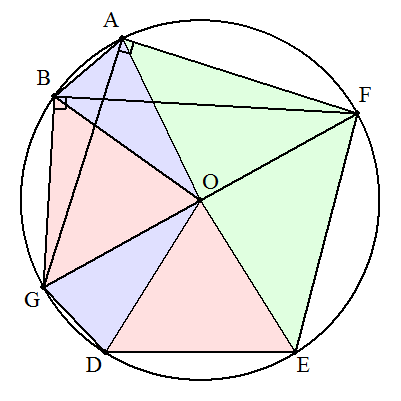
  17. 円の中心をOとし，半径をrとする。
    2個の底辺8の二等辺三角形と2個の底辺17の二等辺三角形と2個の底辺22の二等辺三角形とに分ける。
    次に，6個の二等辺三角形のうち，△OBCと△OCDを入れ換えて，右の図のようにそれぞれ，△OGD，△OBGとする。
    FGは直径となる。
    直角三角形FAG，FBGに三平方の定理を適用して，
    AG＝√(FG2－FA2)＝√{(2r)2－222}＝2√(r2－121)
    FB＝√(FG2－BG2)＝√{(2r)2－172}＝√(4r2－289)
    四角形ABGFにトレミーの定理を適用すると
    AG・FB＝AB・FG＋FA・BG
    2√(r2－121)・√(4r2－289)＝8・2r＋22・17
    両辺を平方すると
    4(r2－121)(4r2－289)＝4(8r＋187)2
    r>0に注意して整理すると，4r3－837r－2992＝0
    (r－16)(4r2＋64r＋187)＝0
    r>0より　r=16･･･（答）
    （補足）
    一般に，AB=BC=a，CD=DE=b，EF=FA=cのとき，xについての3次方程式
    x3－(a2＋b2＋c2)x－2abc＝0
    の正の解が，直径2rとなる。

  18. (1)　(p-r)(a/b)+q（%）
    (2)　ab/(a+b)（g）　※この結果は，濃度に無関係であることを示している。

  19. x＝162（g），y＝212（g）
    一般化→こちら

  20. 35674（通り）

  21. {(π＋6√3)/12}d

  22. 120(2k-1)t/(k+1)　（分）

  23. 2・3672

  24. （順に）1歳，3歳，6歳，8歳

  25. (1)　略
    (2)　正三角形の1辺　√43
    　BC＝2√43
    （補）AE＝p，EC＝q，AF＝r，FB＝sのとき，
    　正三角形の1辺　(ps＋qr)/√(3p2＋q2)

  26. 5√97/16
    （補足）AE＝77/16，AF＝73/16

  27. 2√(39/7)
    （補足）HB＝13，BC＝2√(1027/7)

  28. (1)
    点Pを点A中心に－120°回転させた点をQとすると，
    △APC≡△AQBより，BQ＝CP＝4
    △APQに余弦定理を適用して
    PQ2＝2(√3)2－2(√3)2cos120°＝9
    PQ>0より，PQ＝3
    △BPQは，三辺の比が3：4：5の三角形となるから，∠PQB＝90°
    また，∠AQP＝(180°－120°)/2＝30°
    よって　∠AQB＝120°となるから，△QBAに余弦定理を適用して
    AB2＝(√3)2＋42－2√3・4・cos120°＝19＋4√3
    △ABC＝(1/2)AB2sin120°＝(19＋4√3)/4･･･（答）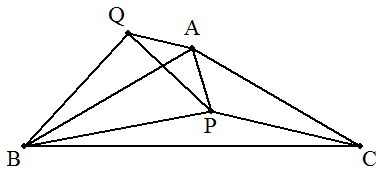
    (2)
    点Pを点A中心に－120°回転させた点をQとすると，
    △APC≡△AQBより，BQ＝CP＝8
    △APQに余弦定理を適用して
    PQ2＝2・52－2・52cos120°＝75
    PQ>0より，PQ＝5√3
    △BPQについて，
    cos∠PQB＝{(5√3)2＋82－(√19)2}/（2・5√3・8）＝√3/2
    0°<∠PQB<180°より，∠PQB＝30°
    また，∠AQP＝(180°－120°)/2＝30°
    よって，∠AQB＝30°＋30°＝60°
    △QBAに余弦定理を適用して
    AB2＝52＋82－2・5・8・cos60°＝49
    △ABC＝(1/2)AB2sin120°＝49√3/4･･･（答）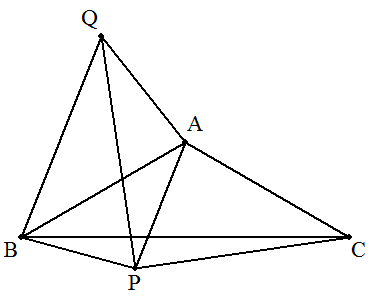

  29. DA，CBの交点をOとし，A，P，DからBCに下ろした垂線の足を
    それぞれH，I，Jとおく。
    いま，DP：PA＝m：nとし，AH＝x，PI＝y，DJ＝zとおくと，
    OA：OP＝OA：(OA＋AP)＝x：yより，AP＝(y/x-1)OA
    OP：OD＝OP：(OP＋PD)＝y：zより，PD＝(z/y-1)OPであるから
    AP：PD＝(y/x-1)OA：(z/y-1)OP＝(y-x)：(z-y)＝n：mより
    y＝(mx+nz)/(m+n)
    △ABC：△PBC：△DBC＝x：y：zであるから
    △PBC＝(m△ABC+n△DBC)/(m+n)　･･･①
    次に，△ABE＝S1，△CDE＝S2，△EBC＝S3，凹形四角形PBEC＝S
    とおくと，①より
    S＋Ｓ3＝{m(S1＋Ｓ3)+n(S2＋Ｓ3)}/(m+n)
    よって　Ｓ＝(mS1+nS2)/(m+n)　･･･②
    ②に，m=1，n=2，S1＝1，S2＝5を代入すると，S＝11/3　･･･（答）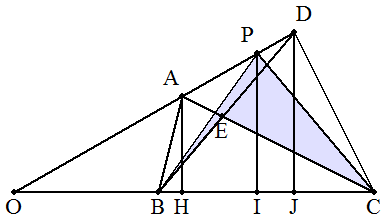

  30. (1)　112
    (2)　3，1，4，6，2，5　　（8通りある。）
    (3)　1，16，2，8，32，4　　（8通りある。）
    解説→こちら

  31. (1)　√7
    (2)　√(25＋12√3)

  32. √7

  33. 1.中心Oをとる。
    2.半径1の円を描く。
    3.一つの直径ABを引く。
    4.ABに直交するもう一つの直径をDOCとする。
    5.OBの中点Mをとる。
    6.Mを中心として，半径MBの円を描く。
    7.この円とCMとの交点をEとする。
    8.Cを中心，CEを半径とする円を描き，Oを中心とする円との交点をP，Qとする。
    9.2点PQを結べば，これが正五角形の1辺となる。
    10.このPQの長さで円弧を切っていく。
    11.正五角形PQRSTの作図が完成。
    （補足）
    1辺aの正五角形を作図するには，半径を√{(5+√5)/10}a＝0.85.6507aとする。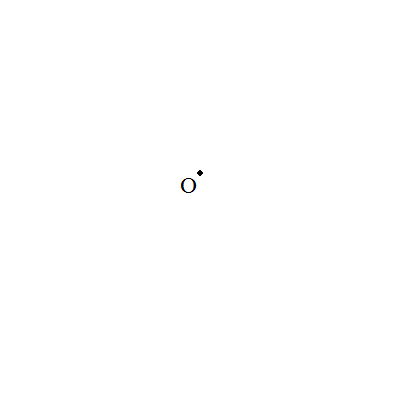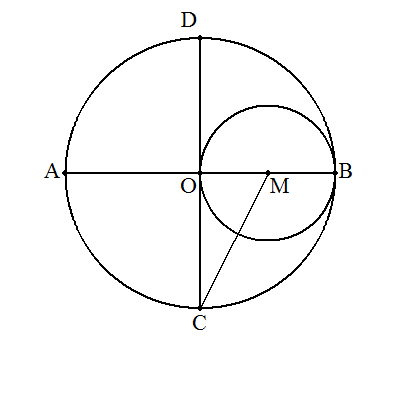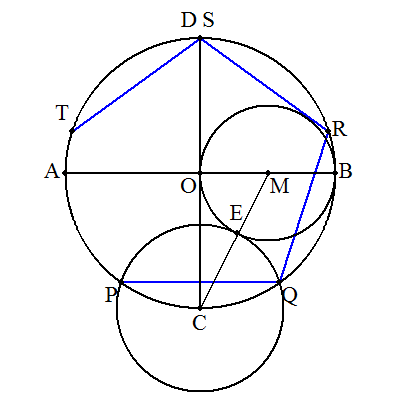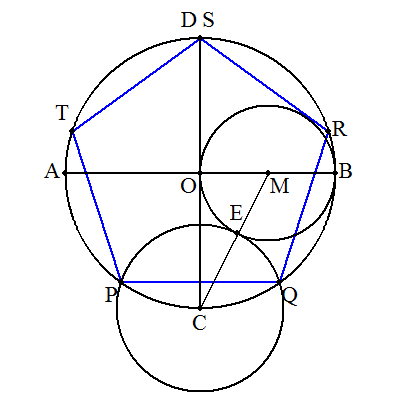

  34. (1/2)[a±b√{4-a2/(4r2-b2)}]
    （例）a＝18,b＝13,r＝65/8のとき，DA，AB＝4,14（2006年東大）

  35. CからFGに下ろした垂線の足をHとする。
    いま，FG＝x，CH＝yとおくと，FH＝(x-a)/2。
    ∠FCH＝18°であるから，tan18°＝FH/CH＝(x-a)/2y･･･①
    正五角形の面積をSとおくと，四角形FCDGは等脚台形であるから，
    仮定より(x+a)y/2＝S/2より，S＝(x+a)y･･･②
    ①，②を辺々掛け合わせると
    Stan18°＝(x2-a2)/2
    x2＝a2＋2Stan18°･･･③
    ここで，正五角形の外接円の半径をrとおくと，正弦定理より
    r/sin54°＝a/sin72°
    r＝asin54°/sin72°＝acos36°/2sin36°cos36°＝a/2sin36°
    であるから，
    S＝5×(1/2)r2sin72°
    ＝(5/2)(a2/4sin236°)×2sin36°cos36°
    ＝(5/4)a2tan54°
    これを③に代入すると
    x2＝a2＋(5/4)a2tan54°tan18°
    ここで，tan18°＝√(25－10√5)/5，tan54°＝√(25＋10√5)/5
    であるから，tan18°tan54°＝√5/5
    x2＝a2＋2×(5/4)a2×√5/5
    よって，x＝FG＝{√(4+2√5)/2}a･･･(答)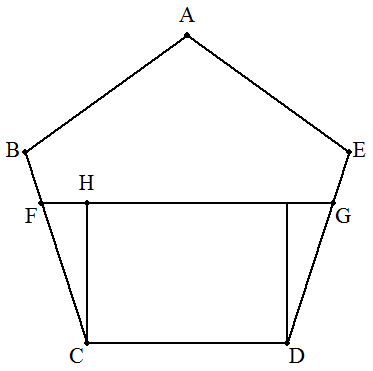

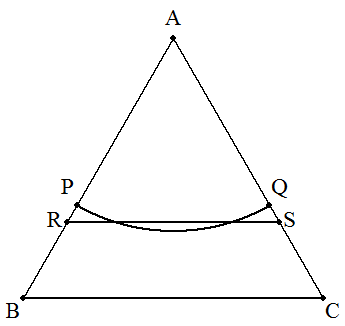
  36. 最小の長さとして考えられるのは，
    ①Aを中心とする弧PQか②BCに平行な線分RSである。
    正三角形の1辺をaとする。
    ①　Aを中心とする扇形の半径をrとすると，
    (1/6)πr2＝(1/2)×(√3/4)a2
    r＝√(3√3/4π)a
    弧PQ＝(1/6)×2πr＝√(π/4√3)a＝0.6733a
    ②　RS＝xとすると，
    (√3/4)x2＝(1/2)×(√3/4)a2
    x＝(√2/2)a＝0.7071a
    よって，弧PQが最小となる。
    （説明）
    面積が一定で周の長さが最小になるのは円であるから。


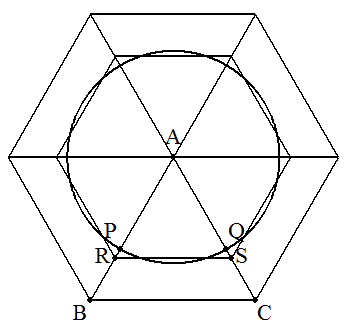
  37. (1)　3/4<rR<3
    (2)　r=√15/4

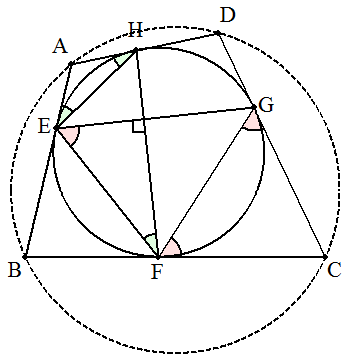
  38. ∠EFH＝α，∠FEG＝βとおくと，α＋β＝90°
    接弦定理より
    ∠AEH＝∠AHE＝α，∠CFG＝∠CGF＝β
    ∠A＋∠C＝(180°－2α)＋(180°－2β)
    ＝360°－2(α＋β)
    ＝360°－2×90°＝180°
    よって，四角形ABCDは円に内接する。
    B139の補足より，
    S＝√(4・6・5・3)＝6√10･･･（答）

  39. (1)　106個
    (2)　280個

  40. pq-3

  41. 証明例→こちら

  42. 9：(5+√61)

  43. (1)　証明略。面積で考えると簡単。一定な値は，正三角形の高さとなる。
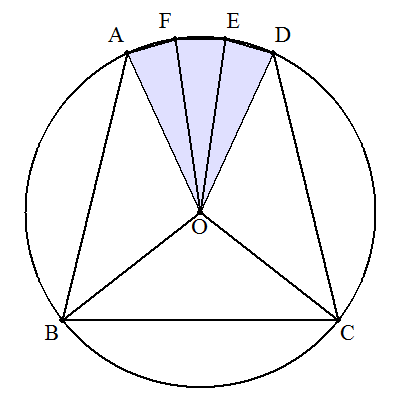
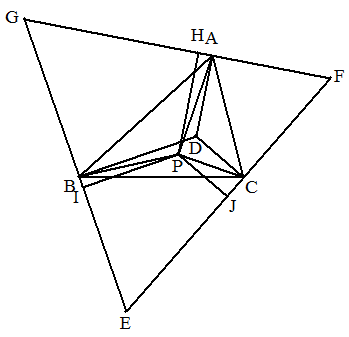
    (2)　求める点は，∠BDC＝∠CDA＝∠ADB＝120°を満たす点。
    （フェルマー点）
    （証明）図のように，点Aを通りDAに垂直な直線，
    点Bを通りDBに垂直な直線，
    点Cを通りDCに垂直な直線でできる三角形をEFGとする。
    △EFGは正三角形となる。
    △ABC内の点Pから，FG，GE，EFに下ろした垂線の足を
    それぞれH，I，Jとする。このとき，
    PA＋PB＋PC≧PH＋PI＋PJ＝DA＋DB＋DC　∵(1)より
    よって，PA＋PB＋PCが最小になるのは，
    点Pが点Dに一致するときである。

  44. {(1-k)(1-l)(1-m)+m}：(1-k)(1-l)m

  45. {(1-m)(1-n)+kn}：{(1-k)(1-l)+lm}

  46. 4：6：3
    （補足）
    与えられた比を順にk：(1-k)，l：(1-l)，m：(1-m)，n：(1-n)とすると，
    AP：PQ：QC＝k(1-n)(1-l+m)：(1-l-n-km+kn+lm+ln+klm-kln+kmn-lmn)：m(1-l)(1-n+k)
    問題は，k=1/2，l=1/4，m=1/3，n=1/5の場合である。

  47. a：(1-a-b)：b
    この問題は，A346の一般化である。

  48. 縦一列の和が369である。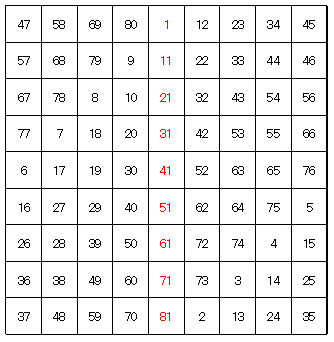

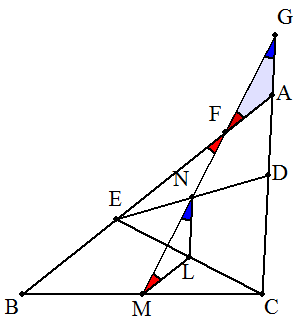
  49. （略証）
    CEの中点をLとすると，中点連結定理より
    LM＝LNより∠LMN＝LNM
    錯角，対頂角，同位角は等しいから
    ∠AFG＝∠AGF
    よって，三角形AFGは二等辺三角形となる。

  50. 並べ方･･･1段目から，俵積みに6枚，5枚，6枚，5枚，･･･と17段積み，最後の1段は1枚ずつ6枚並べる。
    底面積･･･ 12cm×32cm＝384cm2
    解答例→こちら