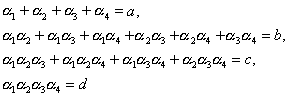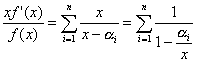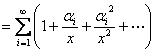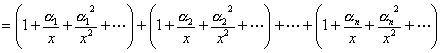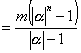対称式や、漸化式、導関数を利用する求め方について解説する。
(1)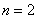 のとき のとき
| 解と係数の関係で | 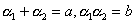 | と置くと、 |
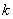 | 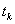 |
| 0 | 2 |
| 1 | 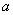 |
| 2 | 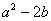 |
| 3 | 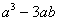 |
| 4 | 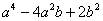 |
| 5 | 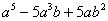 |
| 6 | 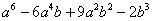 |
| 7 | 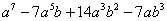 |
| 8 | 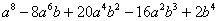 |
| 9 | 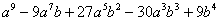 |
| 10 | 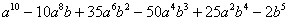 |
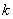 | 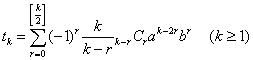 (時岡作) (時岡作)
|
(2)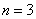 のとき のとき
| 解と係数の関係で | 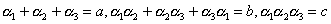 | と置くと、 |
(3)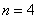 のとき のとき
解と係数の関係で
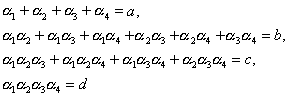
と置くと、
| 3次方程式 | 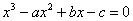 | の場合を考えてみよう。 |
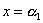 | は解なので、 | 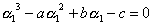 |
| 両辺に | 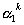 | を掛けると、 | 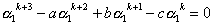 | …① |
| 同様に、 | 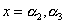 | も解なので、 |
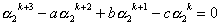 | …② |
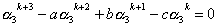 | …③ |
①~③を辺々加えると、
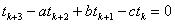 | ∴ | 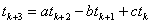 | …④ |
| ここで、 | 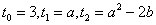 | であるから、④の漸化式を用いると、 |
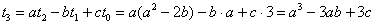
| 順次、 | 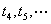 | と求めることができ、その結果は、1(2)の表の通りである。 |
 | として、 |  | と置ける。 |
両辺の絶対値をとってから対数をとると
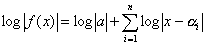
| 両辺を | 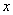 | で微分すると、 |
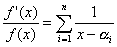
| 両辺に | 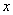 | を掛けると、 |
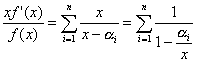 | …⑤ |
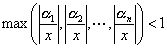 | なる十分大きい | 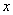 | に対して(※)、⑤の右辺は、 |
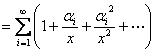
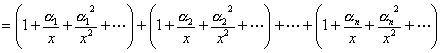
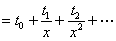
| ∴ | 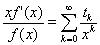 |
| 【例題】4次方程式 | 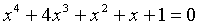 | の4つの解の10乗の和を求めよ。 |
|
| 【解】 | 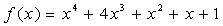 | と置くと、 |
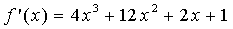 | であるから、 |
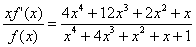
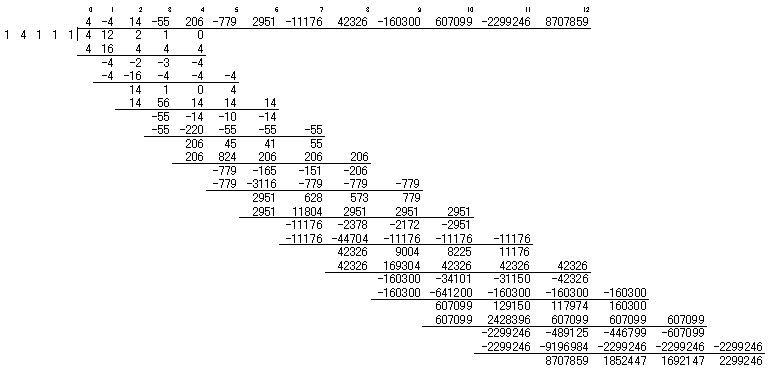
よって、4つの解の10乗の和は、607099…【答】
| (※) | 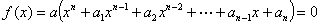 | の一つの解を | 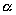 | とするとき、 |
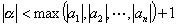 | が成り立つことを証明する。 |
| これが証明されると、 | 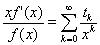 | は実際、 |
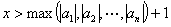 | なる | 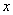 | で成り立つことになる。 |
| 【証明】 | 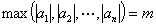 | とおく。 |
| 今仮に | 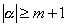 | …⑥と仮定する。 |
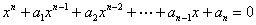 | より、 |
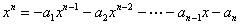
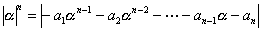
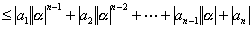
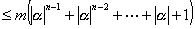 | ∵ | 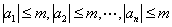 | より |
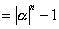
| よって、 | 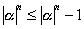 | となり、この不合理は⑥の仮定が原因である。 |
| 従って、 | 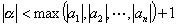 | 【終証】 |
(2002.11.3)
|
![]() のとき
のとき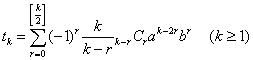 (時岡作)
(時岡作)
![]() のとき
のとき![]() のとき
のとき