| ■Wallisの公式 | にまつわる話 |
- はじめに
私の高校時代の趣味は、数学の問題を作成して、先生方に解いてもらうことでした。作成した問題は「趣味の数学問題集A/B/C」として、現在、「数学のいずみ」のホームページで公開されています。
そのホームページを見てくれた高校3年生のYさんから、平成14年9月27日に質問がありました。それは、C問題31に関連して、次の無限乗積を証明して欲しいというものでした。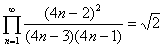
これについて、2、3日考えて、私なりの解答をYさんに示しました。
Yさんは、今年3月から趣味の数学問題集のA問題、B問題と順に解いていき、C問題31(2)④で躓いたそうでです。それは、公開していた私の問題にミスがあったためで、それに気がつくほどの相当の力の持ち主です。
電子メールで何度かやり取りをして分かったことですが、大学(数学科)に進学したらYさんも自作の問題(100題以上)をインターネットに公開したいと書いてありました。その日が待ち遠しいです。
さて、Yさんに示した解答とその証明に用いたWallisの公式についてまとめることにしました。
まず、Wallisの公式は、趣味の数学問題集C問題31に出てくる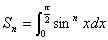
を利用すれば証明できます。
- 証明
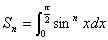
において、 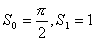
で、 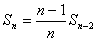
・・・① である。 ①の両辺に 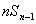
をかけると、 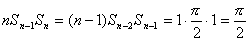
・・・② 次に、 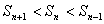
の両辺に 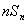
をかけると、 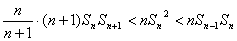
であるから、 ②より、 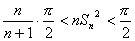
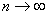
のとき、 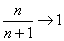
であるから、 ∴ 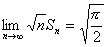
一方、①より
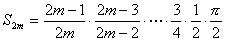
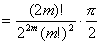
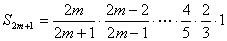
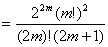
である。
(ア) 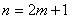
のとき、 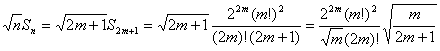
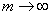
のとき、 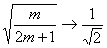
であるから、 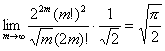
より ∴ 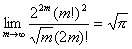
(イ) 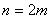
のときも、同様に示される。 【終証】 - Wallisの公式から導かれる無限乗積の例
(1) 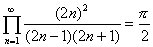
(2) 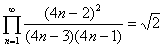
- (1)の証明
証明すべき等式の左辺
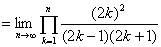
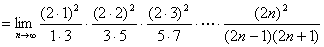
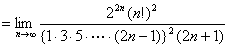
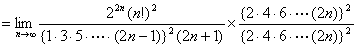
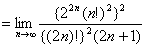
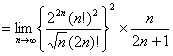
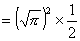
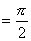
【終証】 - (2)の証明
さて、証明すべき等式の左辺Wallisの公式において、 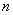
を 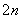
に置き換えると、 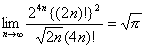
である。 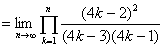
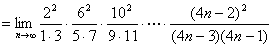
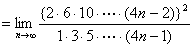
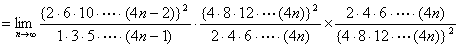
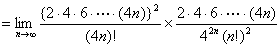
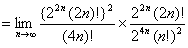
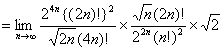
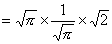
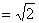
【終証】 - おわりに
趣味の数学問題集はマイナーながら結構見ている人がいるようです。
平成13年4月には、「初等数学の会」の世話人の方から、問題借用の件で問い合わせがありました。勿論許諾しました。A問題31は実際に雑誌「初等数学」の42号に問題が載り、43号に解答と講評が載りました。ホームページでは、「6.今月の課題問題00/01年 」の「課題問題/第42号/2001年8月/明日葉号より」に掲載されています。また、「7.今月の課題問題02/03年 」の「課題問題/第46号/2003年4月/桜草号より」にも掲載されています。
平成13年12月には、いちサラリーマンの男性からB問題9(1)について質問を受けました。
しかし、今回のように高校生からの質問は初めてで、一番嬉しかったです。「この問題集は、数学をこよなく愛する生徒に刺激を与えるものとなることを願っている。」これがそもそも趣味の数学問題集を公開したねらいでもあるからです。(2002.10.1)(2015.3.25)