■趣味の数学問題集・Ｃ問題

  1. 容積が一定の直円錐の容器を作り，その側面の面積を最小にしたい。
    直円錐の底面の半径と高さの比を求めよ。

  2. 半径rの球に直円錐が内接している。
    その体積が最大になるとき，直円錐の底面の半径と高さの比を求めよ。
    また，その時の直円錐と球の体積の比を求めよ。

  3. 直円錐に半径rの球が内接している。
    直円錐の体積が最小になるとき，直円錐の底面の半径と高さの比を求めよ。
    また，その時の球と直円錐の体積の比を求めよ。

  4. AD∥BCである台形ABCDのBC上に点Pをとり，
    BDとAPとの交点をQとする。△QDAと△QBP
    との面積の和が最小になるとき，
    (1)　BPの長さをADの長さで表せ。
    (2)　点Pの位置を作図で求めよ。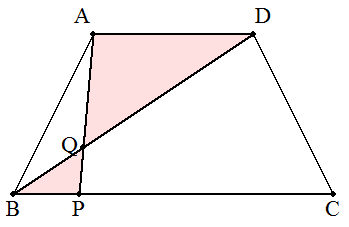

  5. 長方形ABCDのBCの延長上に点Eをとり，
    AEとCDとの交点をFとする。△AFDと△EFC
    との面積の和が最小になるとき，
    (1)　CEの長さをADの長さで表せ。
    (2)　点Eの位置を作図で求めよ。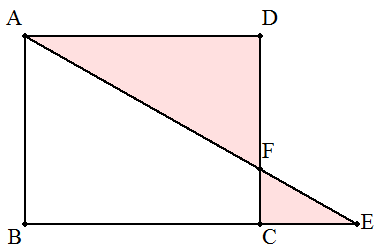

  6. aを定数とする3直線 x-ay+a2=0，ax+a2y+1=0，a2x+y+a=0 でつくられる三角形の面積をSとおく。
    (1)　Sをaを用いて表せ。
    (2)　Sの値によって，aの値の個数を求めよ。
    (3)　あるSの値になるaの値が4個あるとき，Sとaの値をそれぞれ求めよ。

  7. AさんとBさんがコインをn回ずつ投げるゲームをした。
    表が出た回数の多い方が勝ち，同じなら引き分けとする。
    (1)　Aさんが勝つ確率を求めよ。
    (2)　引き分けになる確率をP(n)とおく。
    　n→∞のとき，P(n)√nの極限値を求めよ。

  8. 次の式を簡単にせよ。
    (1)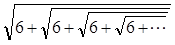　
    (2)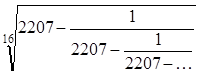　


  9. 第1象限にある楕円x2/a2+y2/b2=1上の点Pにおける
    接線とx軸，y軸との交点をそれぞれA，Bとする。
    線分ABの最小値を求めよ。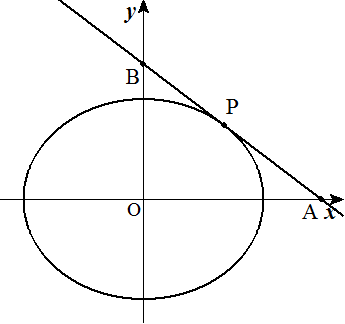

  10. a＜bのとき，f(x)=(x－a)2(x－b)2/x2－c2について，
    方程式f(x)=kの実数解の個数を求めよ。


  11. a＞0，ab-h2＞0，af2-bg2＞0のとき，x，yについての2次式 ax2+2hxy+by2+2gx+2fy+c の最小値mをhの関数とみて，mの最大値を求めよ。


  12. 次の極限値を求めよ。



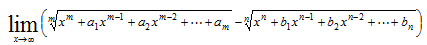
  13. AB＝AD＝a，CB＝CD＝b（0＜a＜b）である凧形四角形ABCDについて，
    BD＝xのときの内接円の半径をr(x)とおく。
    (1)　r(x)を求めよ。
    (2)　r(x)の最大値とそのときのxの値を求めよ。
    (3)　(1)で求めた式で，r(0)，r(2a)の値を定義する。xが0から2aまで変化
    　　するときのr(x)の平均値を求めよ。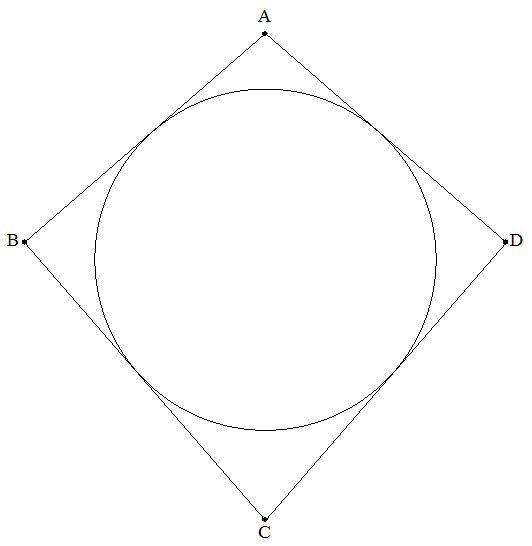





  15. n次関数y=f(x)は，x=0で極大値3，x=4で極小値-5をとり，点（2，-1）は変曲点で，
    この点における接線の傾きは0である。このようなy=f(x)を一つ示せ。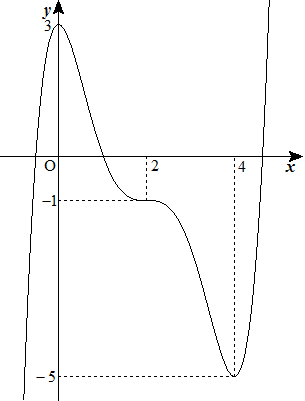


  16. 分数関数y=f(x)は，x=0で極大値3，x=4で極小値-5をとり，点（2，-1）は変曲点で，
    この点における接線の傾きは0である。また，x→±∞のとき，y→-1である。
    このようなy=f(x)を一つ示せ。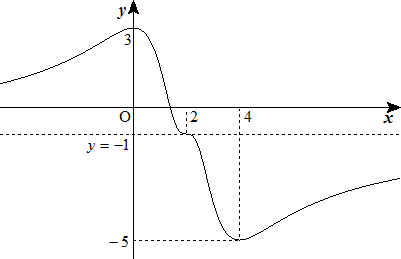


  17. 次を証明せよ。



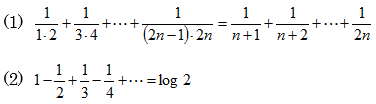
  18. 4次方程式x4+ax+b=0（ab≠0）の4つの解のn乗の和をanとおくとき，次の比例式を証明せよ。
    a3a10：a4a9：a6a7：a13=30：12：21：13


  19. 楕円x2/a2+y2/b2=1上の点Tにおける接線に原点から
    下した垂線の足をPとする。
    (1)　点Pの軌跡の方程式を求めよ。
    (2)　点Pの軌跡によって囲まれる図形の面積Sを求めよ。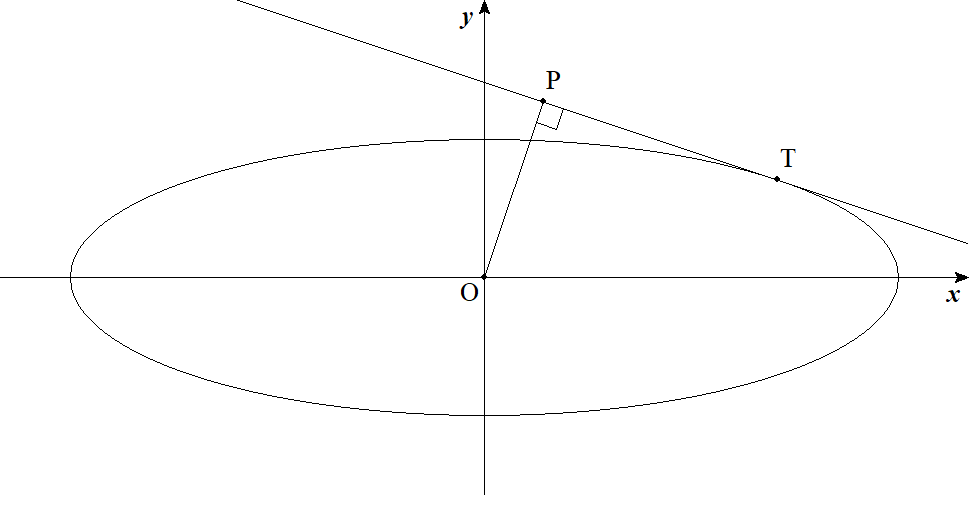


  20. 双曲線x2/a2-y2/b2=1（a＞b＞0）上の点Tにおける接線に
    原点から下した垂線の足をPとする。
    (1)　点Pの軌跡の方程式を求めよ。
    (2)　点Pの軌跡によって囲まれる図形の面積Sを求めよ。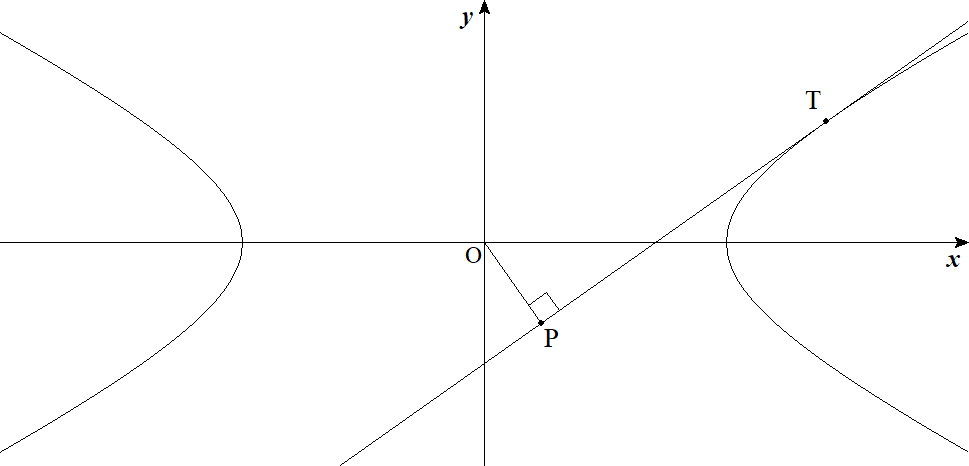


  21. 自然数aをn個つなげた数をa(n)で表す。（例）12(3)＝121212
    このとき，√1(2020)の小数第1011位を求めよ。


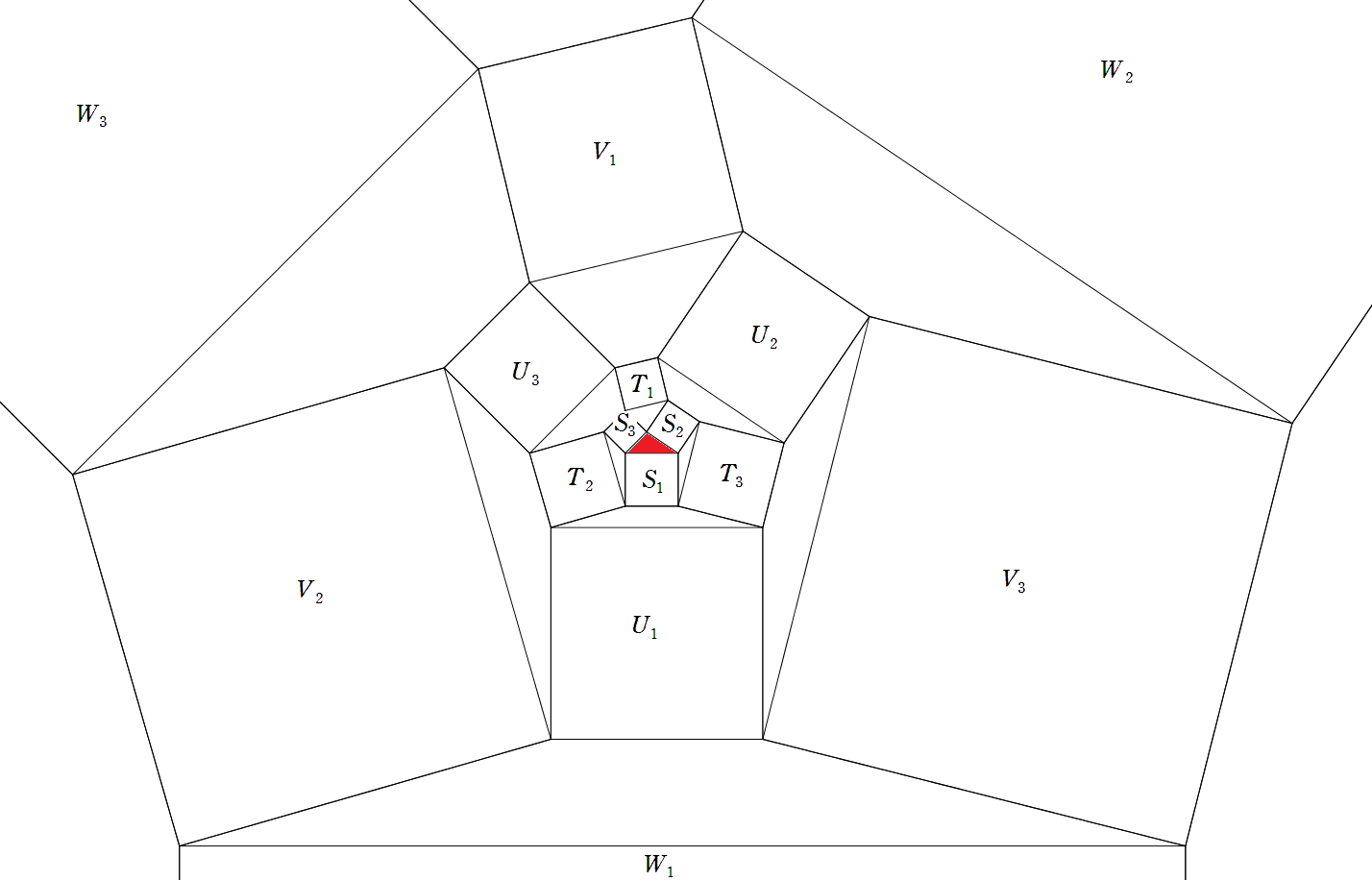
  22. △ABCの3辺をa，b，c，3つの中線をAD1＝d1，BD2＝d2，CD3＝d3とする。
    三角形の外側に3個の正方形S1，S2，S3をつくり，さらに下の図のように
    外側に3個の正方形T1，T2，T3，さらに外側に3個の正方形U1，U2，U3，…
    と次々につくる。このとき，
    (1)　d1，d2，d3をa，b，cを用いて表せ。
    (2)　正方形T1の1辺をｄ1等を用いて表せ。
    (3)　正方形U1の1辺をa，b，cを用いて表せ。
    (4)　正方形V1の1辺をｄ1等を用いて表せ。
    (5)　正方形W1の1辺をa，b，cを用いて表せ。
    (6)　正方形X1の1辺をｄ1等を用いて表せ。
    (7)　正方形Y1の1辺をa，b，cを用いて表せ。
    (8)　正方形Z1の1辺をｄ1等を用いて表せ。
    (9)　正方形AA1の1辺をa，b，cを用いて表せ。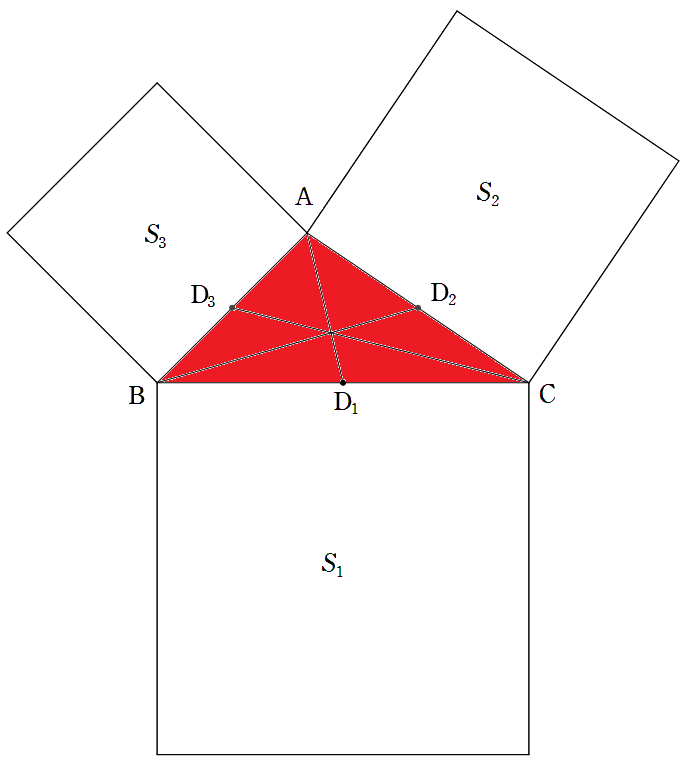




  23. △ABCのCA，AB上にそれぞれ点D，Eを，DE∥CBとなるようにとる。
    このとき，△DEF/△ABCの最大値を求めよ。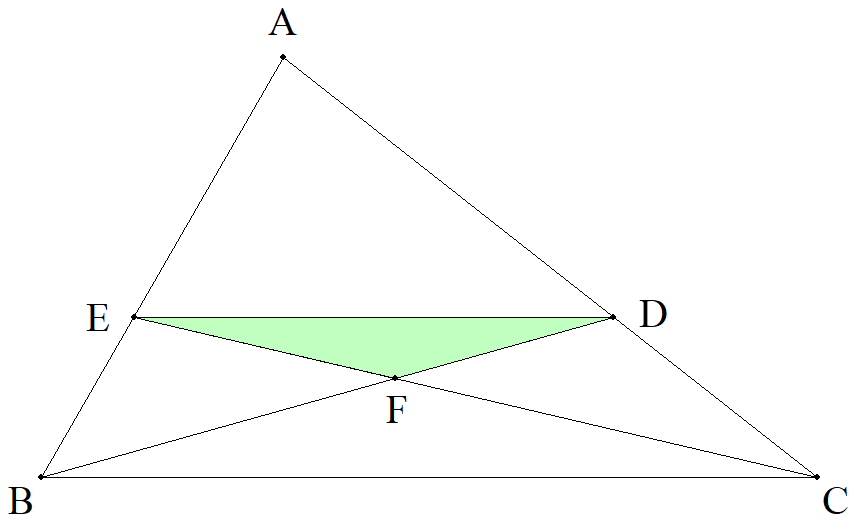



  24. e=1+1/1!+1/2!+1/3!+…（自然対数の底）は無理数であることを証明せよ。





  26. 2曲線y=logx，y=(logx)2によって囲まれる部分の面積を求めよ。


  27. 1辺の長さが1である正三角形の各頂点から辺に
    xの長さとり，斜線を引いて正三角形を分割し，
    赤の四角形の面積の和をS(x)とおく。
    (1)　S(x)をxを用いて表せ。
    (2)　S(x)が最大になるときのxの値を求めよ。
    (3)　S(x)の最大値をxの最低次の整式で表せ。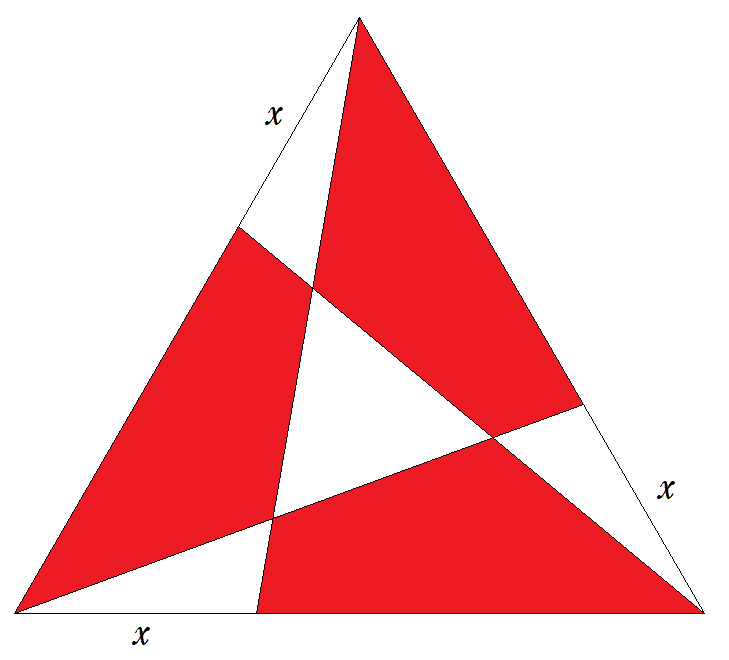



  28. 1辺の長さが1である正方形の各頂点から辺に
    aの長さとり，斜線を引いて正方形を分割し，
    赤の四角形の面積の和S(a)の最大値とそのと
    きのaの値を求めよ。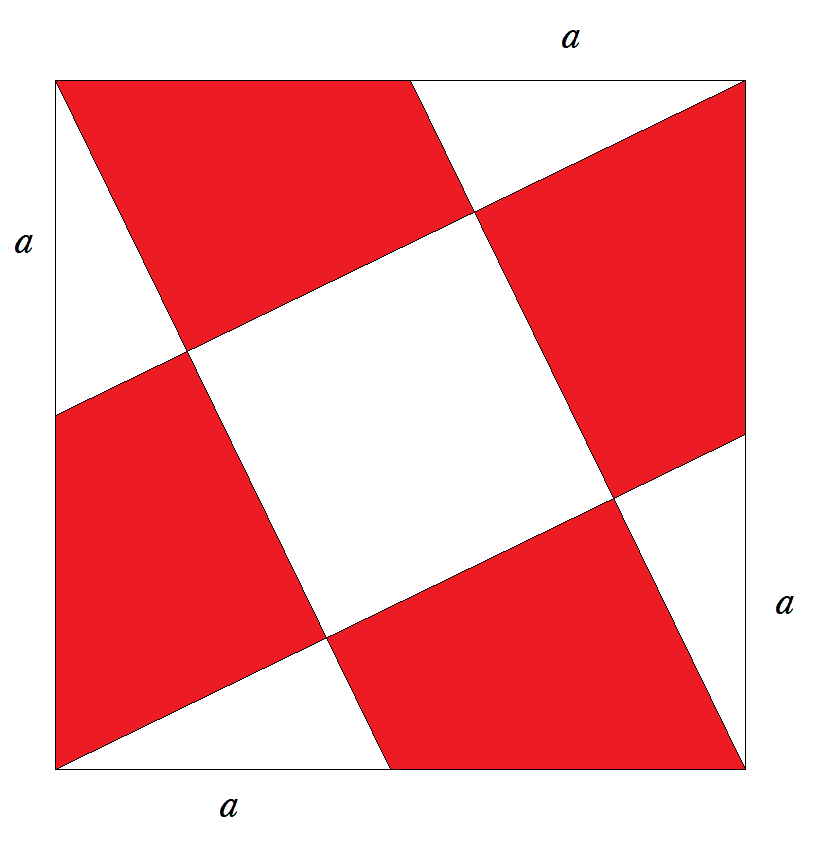