| の四角形 | の面積 | は |
| ( | ) |
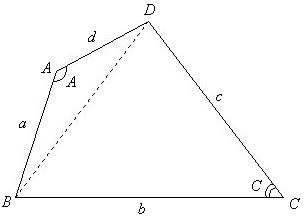
| 【証明】 | と | に余弦定理を適用すると |
| より |
| ・・・① |
| であるから |
| より |
| ・・・② |
| であるから |

| ・・・③ |
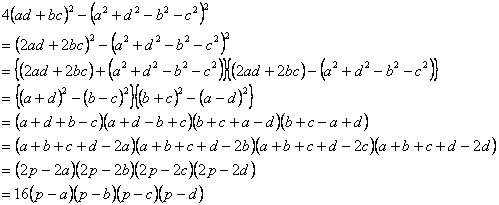
| 【終証】 |
| | が一定のとき,四角形の面積が最大となるのは, | のときである。 |
| このとき, | となり,四角形 | は円に内接する。 |
| 四角形 | が円に外接すれば, | である。 |
| このとき |
| であるから |
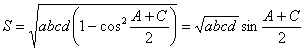
| 特に,四角形 | が円に内接して外接すれば, | であるから |
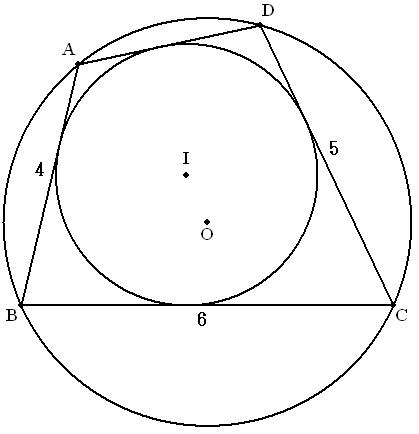
| 四角形 | が円に内接して外接している。 |
| のとき,次の問いに答えよ。 |
| (1) | の長さを求めよ。 |
| (2) 四角形 | の面積を求めよ。 |
| (3) 内接円の半径 | を求めよ。 |
| (4) 外接円の半径 | を求めよ。 |
| ∴ | ・・・(答) |
| (2) | ・・・(答) |
| (3) | より | 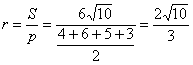 | ・・・(答) |
| (4) | , |
| より |
| ・・・(答) |