| ■不定積分 | を求めよ。 |
| 【解】 | と置くと、 |
| 両辺を | ∴ |
| 次に、 | と置くと、 |
| であるから(※)、 |
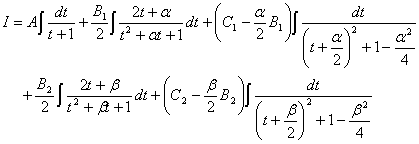
ここで、
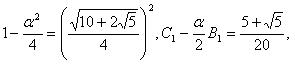
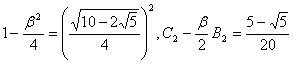
である。
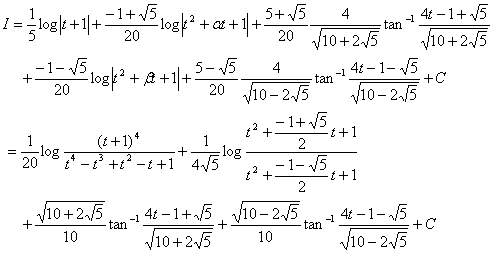
| 最後に、 | を代入すると、 |
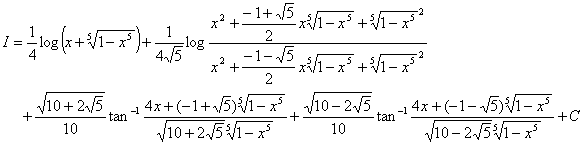
・・・【答】
| (※) | ・・・①と置く。 |
| まず、 | と置くと、 |
| 係数を比較して、 |
| よって、 | は、 |
| より、 | である。 |
| ・・・② |
| ∴ | ・・・③ |
| ( | | ・・・④ |
| ( | | ・・・⑤ |
| ( | | ・・・⑥ |
| (定数項) | | ・・・⑦ |
| ・・・⑧ |
| ・・・⑨ |
| ⑤-⑦ | | ・・・⑩ |
| ⑥-④ | | ・・・⑪ |
| ⑧、⑩を連立させて、 |
| ⑨、⑪を連立させて、 |
| よって、 |
補足
- 不定積分
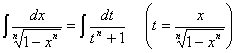
- 不定積分
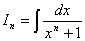
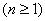
について 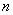
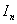
1 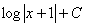
2 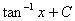
3 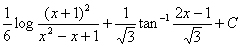
4 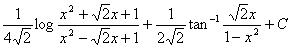
5 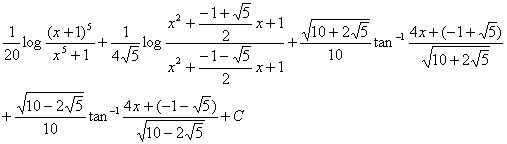
6 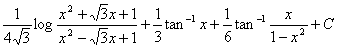
- 定積分
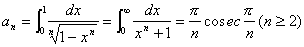
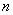
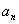
2 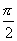
3 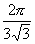
4 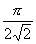
5 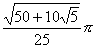
6 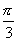
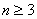 のとき、
のとき、
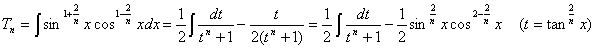
【例】不定積分 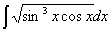
を求めよ。
【解】 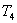
の場合である。 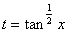 と置くと、
と置くと、
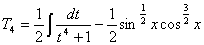
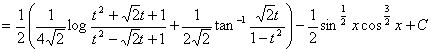
(補足2) 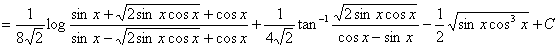
・・・【答】
(2002.10.31/Update 2002.11.6)