■人の中に同じ誕生日の人がいる確率について（ただし，2月29日生れの人はいないものとする。）
求める確率をとおくと，は明白であるから，
の場合を考える。
同じ月日に生れた人のいる事象の余事象は，同じ月日に生まれた人がいない事象である。
その確率を計算する。
人分の異なる誕生日の選び方は通り
選んだ人はその個の誕生日のどれかになればいいので，その順列は通り
よって，余事象の起こる場合の数は，通り
また，起こり得るすべての場合の数は，通り
従ってより

これを計算すると次の表のとおりである。
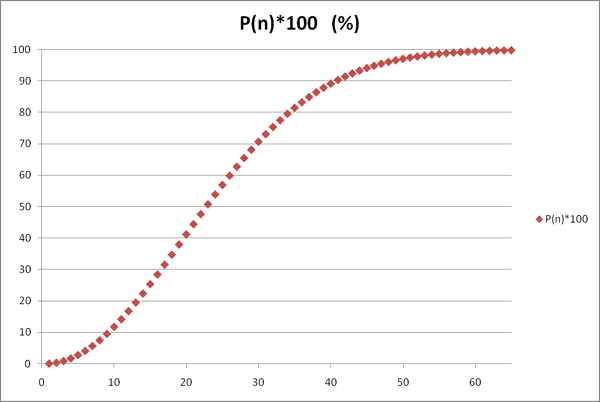
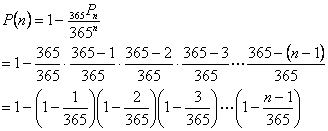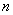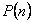10
20.002739726
30.008204166
40.016355912
50.027135574
60.040462484
70.056235703
80.074335292
90.094623834
100.116948178
110.141141378
120.167024789
130.194410275
140.223102512
150.25290132
160.283604005
170.315007665
180.346911418
190.379118526
200.411438384
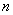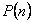210.443688335
220.475695308
230.507297234
240.538344258
250.568699704
260.59824082
270.626859282
280.654461472
290.680968537
300.706316243
310.730454634
320.753347528
330.774971854
340.795316865
350.814383239
360.832182106
370.848734008
380.864067821
390.878219664
400.89123181
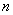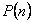410.903151611
420.914030472
430.923922856
440.932885369
450.940975899
460.948252843
470.954774403
480.960597973
490.965779609
500.97037358
510.974431993
520.978004509
530.981138113
540.983876963
550.986262289
560.988332355
570.990122459
580.991664979
590.992989448
600.994122661
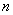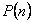610.995088799
620.995909575
630.996604387
640.997190479
650.997683107
660.998095705
670.998440043
680.998726391
690.998963666
700.999159576
710.999320753
720.999452881
730.999560806
740.999648644
750.999719878
760.999777437
770.999823779
780.999860955
790.999890668
800.999914332
810.999933109
820.999947953
830.999959646
840.999968822
850.999975997
860.999981587
870.999985925
880.99998928
890.999991865
900.999993848
910.999995365
920.999996521
930.999997398
940.999998061
950.99999856
960.999998935
970.999999215
980.999999424
990.999999578
1000.999999693
この表から，次のことがわかる。
(1)となる最小のは，。
　 つまり，23人の集団の中には同じ誕生日の人がいる確率が0.507と五分五分強。
(2)35人学級では，である。8割強。
(3)40人学級では，である。9割弱。
(4)となる最小の は，。
(5)となる最小の は，。
(6)となる最小の は，。

（2009/12/09）