■エピサイクロイド（Epicycloid）外サイクロイド
　原点を中心とする半径の円に半径の円が外接しながらすべることなくころがるとき，
動く円の周上に固定した点で，はじめ軸上にあった点の位置は次の式で与えられる。
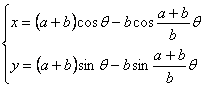…①

【証明】

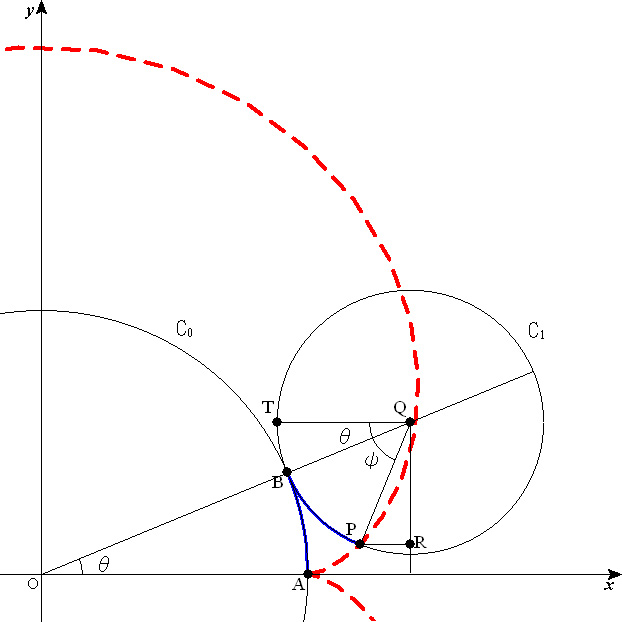
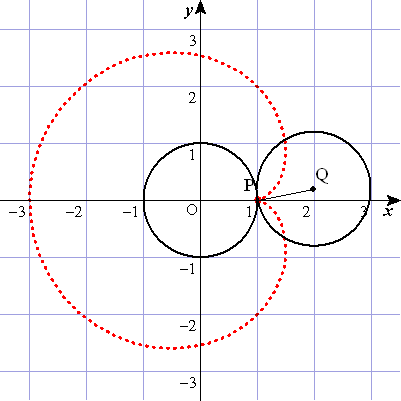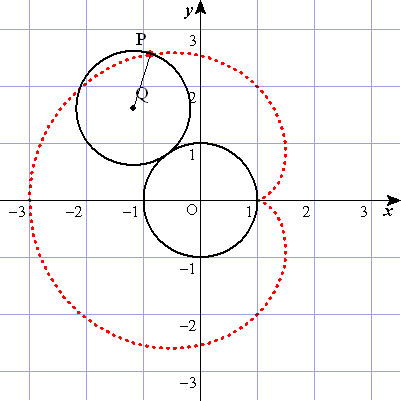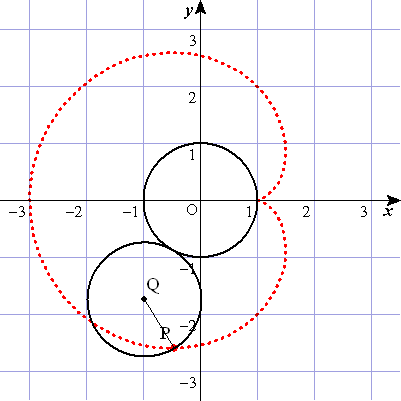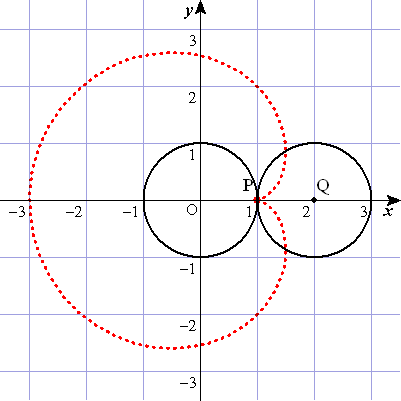
図で，とおくと，点の座標は，である。
図のように，円上に点をとなるようにとる。
また，円の中心から軸に垂線を引き，その垂線上に点をとなるようにとる。
とおくと，弧＝弧であるから，∴
⊿は直角三角形で，であるから，

よって，点の座標は，
点の座標は，となる。
【終証】
（2009.11.1）
【補足】
特にのとき，①はとなり，
この曲線をカージオイド（cardioid心臓形）という。

（下図は の場合）

（2009,11,28）