■三角形に含まれる三角形の面積
Ⅰに内接するの面積(1)
の辺上に
それぞれ点をとり，

とおく。このとき

である。
【証明】
であるから

また，

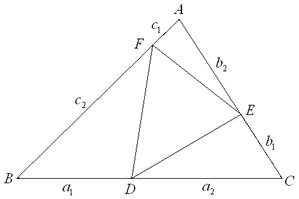であるから

ここで，を代入すると

【終証】
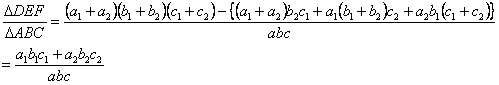
Ⅱに内接するの面積(2)
内に1点をとり，
と，と，と
との交点をそれぞれとする。
このとき，

である。
【証明】
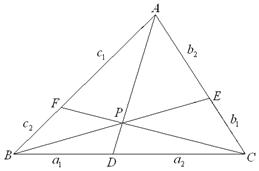Ⅰでチェバの定理より，であるから，
よって，
【終証】
Ⅲ　鋭角三角形において，次の各々の場合におけるの値
(1)は点が重心の場合
(2)は点が外心の場合
(3)は点が内心の場合
(4)は点が垂心の場合
(5)は点が内接円の接点の場合
(6)は点が傍接円の接点の場合
【辺による結果と角による結果一覧】
　
辺
角
辺
角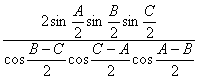
辺
角
辺
角
辺
角
【参考】の大小関係

（等号は正三角形のとき）＜予想＞
【証明】
(1)　3点は各辺の中点であるから，Ⅱの結果を使うと

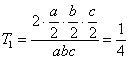
(2)　である。
の両辺をで割ると


∴　
同様に

Ⅱの結果を使うと

ここで

同様に

であるから

(3)　より，Ⅱの結果を使うと

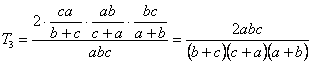
ここでであるから

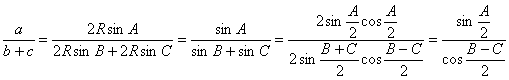
同様に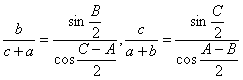

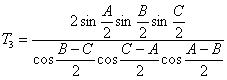
(4)より，Ⅱの結果を使うと

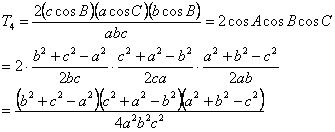
(5)であるから，Ⅱの結果を使うと

またであるから

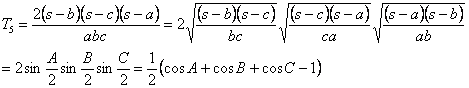
さらにであるから

(6)であるから，Ⅱの結果を使うと
となる。
【終証】
Ⅳ に含まれるの面積
の辺上に
それぞれ点をとり，

とおく。
また，との交点を ，
との交点を，
との交点をとするとき，

である。
【証明】
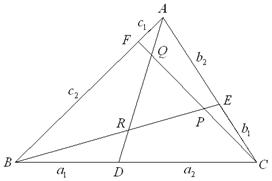とおく。
であるから
　･･･①
[1]　メネラウスの定理よりであるから
よってであるから

∴　･･･②
[2]　同様に，であるから

∴･･･③
[3] 同様に，であるから

∴･･･④
②～④を①に代入すると

ここで

同様にであるから

【終証】
【例題】
の辺上にそれぞれ点をとり，
とおく。
また，との交点を，との交点を，
との交点をとするとき，次の値を求めよ。
(1)(2)
【解答】
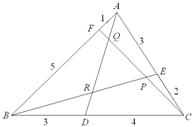(1)であるから
･･･【答】
(2)･･･【答】
　 （補足）ヘロンの公式から

であるから
，
（2009/1/11）